In this first project, we will look at two concepts that are vital to e.g. the compiler you use for writing programs; tokenizing and parsing.
Let’s assume you work in an organization that keeps track of e.g. a large number of books, and wants their users to be able to search among them. Each book has a number of categories associated with it, and your job is to create an application that lets a user specify a condition, such as “Programming and Algorithms”, and ask the system if a specific book fulfills that condition or not, using these categories.
As an example, let’s assume that our database contains the following books, with given categories:
| Book | Categories |
|---|---|
| The C Programming Language | C, Programming |
| The C++ Programming Language | C++, Programming |
| Algorithms in C++ | Algorithms, C++, Programming |
| Artificial Intelligence | AI, Programming |
Let’s look at a few expressions and see which books that fulfill them:
| Expression | Books |
|---|---|
| C | The C Programming Language |
| C OR C++ | The C Programming Language, The C++ Programming Language |
| C AND C++ | – |
| Programming AND C | The C Programming Language |
| C++ | The C++ Programming Language, Algorithms in C++ |
| C++ AND NOT Algorithms | The C++ Programming Language |
Note that a more general (and useful) task would be to let the users write queries that automatically retrieve all articles that fulfill the condition. Doing this in an efficient way is a more difficult task than simply determining if one article matches the condition, and will not be covered. Also note that in a real-life scenario, you would probably not create this application yourself, but use an existing one, perhaps by using a relational database and querying the database using SQL. Since this is a blog about programming however, we will create a system that parses an input string (the specified condition), builds a so called parse tree, and finally matches a set of categories against this tree.
To specify the structure of a language, such as your favorite programming language, or the simple language we will be using for our conditions, you may use a BNF grammar, which you can read more about here. The grammar for our language looks as follows:
Expr ::= '(' Expr ')'
| Expr BinOp Expr
| UnOp Expr
| String
BinOp ::= AND | OR
UnOp ::= NOT
Starting with the line “BinOP ∷= AND | OR”, this means that a binary operator in our language is either “AND” or “OR”. The line “UnOp ∷= NOT” indicates that we have one unary operator, “NOT” that is valid in our language. Looking at the actual expressions (i.e. “complete sentences”) in our language, these may have one of four formats. The first line says that an expression may consist of a “(“ followed by an expression followed by “)”. This recursive definition means that if “A” is an expression then “( A )” is also an expression. The second line says that an expression may consist of an expression followed by a binary operator followed by another expression. This means that if “A” and “B” are valid expressions, then “A AND B” and “A OR B” are both valid expressions as well. The third line in the definition of an expression states that an expression may consist of a unary operator followed by an expression. This means that if “A” is a valid expression, then “NOT A” is also a valid expression. Finally, we see that an expression may be any string.
Let’s look at a few examples, and how they are matched against these rules.
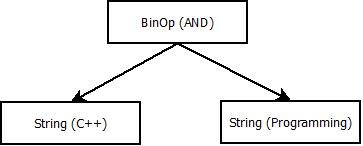
C++ AND Programming. Looking at our rules above, we see that we can match our expression as Expr BinOp Expr where the first Expr (call it E1) is “C++”, the second one (call it E2) is “Programming” and BinOp is AND. Furthermore, we can match both E1 and E2 as strings according to the last version of our Expr rule. We will look deeper into this when we look at building the parse tree, but I can tell you already that the parse tree for this expression will look like:
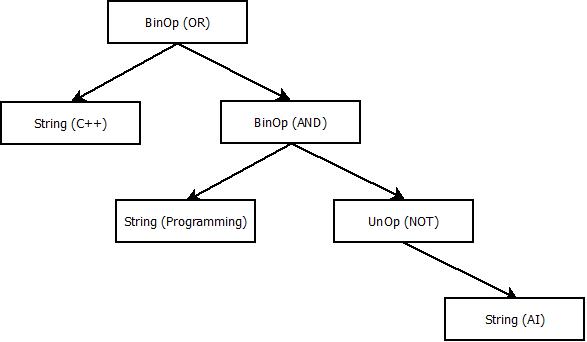
C++ OR (Programming AND NOT AI). We start by trying to match this expression against the first rule, Expr ::= ‘(‘ Expr ‘)’. Since the first and last parts of our expression are not parentheses, we can see that this is not possible. We then try to match it against the second rule for expressions, Expr BinOp Expr. This will succeed, and we get E1 OR E2 where E1 = “C++” and E2 = “(Programming AND NOT AI)”. We try to match E1 against the expression rules, and find that we can match it as a string, which means we are done with it. We try to match E2 against our expression rules, and find that we can use the first rule, getting ( E3 ), where E3 = “Programming AND NOT AI”. E3 can be matched against the second rule, so we get E4 AND E5. In the same way, we match E4 as a string, and E5 as NOT E6. E6, finally, is a string. The parse tree will look as follows:
You may have noticed that the parentheses don’t give any nodes in the tree by themselves; what they do is affect the structure of the existing nodes. Actually, this last example would give us the same parse tree if we skipped the parentheses altogether. However, if we look at the expression (C++ OR Programming) AND NOT AI instead, we would get the following parse tree:
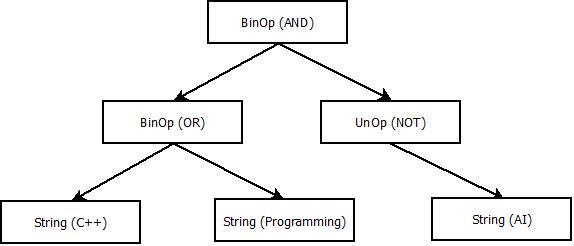
Feel free to match the expression against our rules, and see if you come up with the same tree.
We will create this system in two steps:
- Break up the input text (i.e. “C++ and Programming”) into its individual parts, called “tokens”. This step is called “tokenization”.
- Create the parse tree given these tokens. This step also checks that the entered text represents a valid condition (i.e. that we don’t enter e.g. “C++ AND OR Programming”). The parse tree will include an evaluation method, which lets the user evaluate a set of categories against the parse tree.
In the next post, we will start looking at the tokenization of our input string. We will actually make a more complete tokenizer, which can read a complete text file and break it up into tokens, discarding comments (both single-line and multi-line), retaining information about the original line number for each token. Until then!
